Adição e Subtração (Matemática básica)

 

Operações de adição     

O número surgiu a partir do momento em que existiu a necessidade de contar objetos e coisas e isso aconteceu há mais de 30.000 anos. Os homens nessa época viviam em cavernas e grutas e não existia a ideia de números, mas eles tinham a necessidade de contar. Assim, quando os homens iam pescar ou caçar levavam consigo pedaços de ossos ou de madeira. Para cada animal ou fruto capturado, o homem fazia no osso ou no pedaço de madeira um risco.

           Com a evolução do homem, que deixando de ser nômade fixou-se em um só lugar, esse passou a praticar não somente a caça e a coleta de frutos, mas também o cultivo de plantas e a criação de animais. A partir daí surgiu a necessidade de uma nova forma de contagem, pois o homem precisava controlar o seu rebanho.
Passou-se, então, a utilizar pedras: cada animal representava uma. Mas como isso era feito? Para cada animal que ia pastar, uma pedra era colocada dentro de um saco. Ao final do dia, para cada animal que entrava no cercado, uma pedra era retirada. Assim, era possível manter o controle e saber se algum animal havia sido comido por outro animal selvagem ou apenas se perdido.
Com a evolução do homem e da matemática, surgiu a palavra cálculo, que em latim significa “contas com pedras”.

Operação de adição entre números inteiros

Antes de tratarmos das operações com números inteiros, devemos recordar quais elementos fazem parte desse conjunto. Pertencem ao conjunto dos números inteiros todos os números positivos, negativos e o zero. Sendo assim:

Z = {… - 3, - 4, - 3, - 2, - 1, 0, + 1, + 2, + 3, + 4...}

            Adição de números inteiros: Na adição de números inteiros, somam-se as parcelas:

Primeiramente vamos adicionar esses dois número 3892 + 663, o alinhamento deve ocorre da direita para a esquerda, assim teremos unidade de baixo de unidade e dezena de baixo de dezena.

3892 + 663= 4555   

Operação de adição entre números decimais

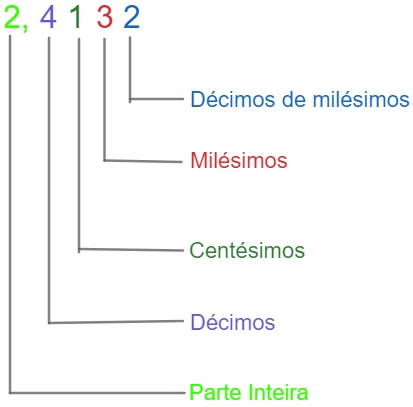
    A fim de facilitar as definições que virão, a seguir estabelecemos algumas nomenclaturas. Um número decimal é formado por sua parte inteira e pela parte decimal. A parte decimal é organizada da seguinte maneira: décimo, centésimo, milésimo, décimo de milésimo, centésimo de milésimo e assim por diante.

Veja o exemplo:

Adição com números decimais

A adição de números decimais é definida de maneira semelhante à adição de números inteiros, nessa operação devemos somar parte inteira com parte inteira, décimos com décimos, centésimos com centésimos, e assim sucessivamente. Em outras palavras, devemos colocar vírgula abaixo de vírgula, veja o exemplo.

Exemplo 1

Vamos determinar a soma dos números 0,65 e 0,792. Lembre-se: o número 0 no final de qualquer número decimal não acresce no valor.

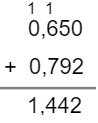
Exemplo 2

Determine o valor da soma 1,442 + 2,4.

 

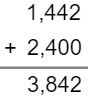
 Propriedades da adição:

As propriedades da adição são: fechamento, comutatividade, associação e elemento neutro.

Comutatividade

Se mudarmos as parcelas de lugar na adição, o resultado não se altera.

7 + 3 = 10

3 + 7 = 10

5 + 4 = 9

4 + 5 = 9

Associação

As parcelas numa adição podem ser somadas de maneiras diferentes, e o resultado não se altera.

(5 + 2) + 6 = 13

5 + (2 + 6) = 13


Elemento Neutro

Na adição, o zero é considerado elemento neutro, assim, qualquer número adicionado a zero tem como resultado o próprio número.

0 + 7 = 7

2 + 0 = 2

4 + 0 = 4

10 + 0 = 10

Fechamento

Quando adicionamos dois ou mais números naturais, o resultado sempre será um número natural.

8 + 6 = 14
8 é um número natural
6 é um número natural
14 é um número natural
 

5 + 11 = 16
5 é um número natural
11 é um número natural
16 é um número natural

Operações de Subtração 

Para subtrairmos dois números decimais, devemos da mesma forma que na adição colocar vírgula de baixo de vírgula. Sendo que o diminuendo deve ser sempre maior que o subtraendo e o resultado recebe o nome de resto ou diferença.

• 7,37 – 2,8 → minuendo e subtraendo nessa mesma ordem.

  6  13
  7 , 3 7 → Minuendo
- 2 , 8 0 → Subtraendo → acréscimo do zero para completar casas decimais.
  4 , 5 7 → Resto ou Diferença

Para subtrair 8 décimos, transformamos 1 inteiro em 10 décimos, ficando com 13 décimos no minuendo. Assim, fazemos:
13 – 8 = 5
6 – 2 = 4 

► 0,25 - 0,18

       1 15
  0 , 2 5
- 0 , 1 8 
  0 , 0 7

Pra subtrair 8, transformamos 1 décimo em 10 centésimos, ficando com 15 o minuendo. Assim, fazemos:
15 – 8 = 7
1 – 1 = 0