Razão, Proporção, escala, grandezas diretamente e inversamente proporcionais

Razão e Proporção

Como estimar a população de peixe na água?

Um método bastante interessante para se estimar a população de peixes em um lago é o seguinte: primeiro, colhe-se uma amostra (A) de peixes desse lago e marcam-se esses peixes. Essa marcação pode ser feita de diversas maneiras, e uma das mais usuais é o implante de um microchip sob a escama de cada peixe coletado. Em seguida, devolvem-se os peixes ao lago. Após um certo período de tempo, é colhida no mesmo lago uma nova amostra (B) de peixes.

Nessa nova amostra, observam-se o número total de peixes coletados e a quantidade de peixes marcados (M). Admitindo-se que a população do lago tenha se mantido constante entre a data da marcação e a da coleta da nova amostragem, pode-se determinar a quantidade total (T) de peixes nesse lago através da proporção:

É claro que esse número fornece apenas uma estimativa da quantidade de peixes, pois, nesse intervalo de tempo, pode ter havido nascimento ou morte de peixes, além de migrações sazonais. Mas, mesmo assim, já é um número muito próximo da quantidade real de peixes.

Esse método também é utilizado para se estimar populações de outros animais em florestas e savanas. E tudo isso graças a um conceito matemático: a noção de razão e proporção.

A palavra RAZÃO pode ser entendida através de um sinônimo de uma operação matemática, chamada divisão. Quando queremos saber a razão entre dois números como o 2 e 3 por exemplo, e só dividi-lo 2/3.

Porém muitas vezes a razões diferente que dão o mesmo resultado, existe várias divisões dando o mesmo resultado, toda vez que isso acontecer podemos pensar em PROPORÇÃO, quando percebemos que 4/6 e 2/3 dá o mesmo resultado, significa dizer que esses números são proporcionais. Então se quisermos saber se dois números são proporcionais é só multiplicarmos eles no formato de crus.

            Saber sobre proporções facilita resolver problemas de forma fácil, através da famosa regra de três. Acompanhe esse probleminha ‘’ Uma vaca tem quatro patas, quantas patas terá 10 vacas?’’ Perceba que existe uma proporção entre o número de pacas e de vacas, quanto mais vacas mais patas. Se pegarmos o 1 e multiplicarmos por X será a mesma coisa que multiplicarmos o 10 por 4, ou seja temo suma proporção. É toda vez que identificamos uma proporção podemos usar a regra de três. 

Questão para fixar o conteúdo de razão e proporção:

1.(ENEM-2014)Boliche é um jogo em que se arremessa uma bola sobre uma pista para atingir dez pinos, dispostos em uma formação de base triangular, buscando derrubar o maior número de pinos. A razão entre o total de vezes em que o jogador derruba todos os pinos e o número de jogadas determina seu desempenho.
Em uma disputa entre cinco jogadores, foram
obtidos os seguintes resultados:
Jogador I – Derrubou todos os pinos 50 vezes em 85 jogadas.
Jogador II – Derrubou todos os pinos 40 vezes em 65 jogadas.
Jogador III – Derrubou todos os pinos 20 vezes em 65 jogadas.
Jogador IV – Derrubou todos os pinos 30 vezes em 40 jogadas.
Jogador V – Derrubou todos os pinos 48 vezes em 90 jogadas.
Qual desses jogadores apresentou maior desempenho?
A) I
B) II
C) III
D) IV
E) V

Escalas

Uma aplicação bastante interessante da regra de três aparecem em escalas, essa já vimos nos livros de história, geografia e principalmente nos mapas.Uma mapa nada mais é do que um fator de conversão minuciosa entre o desenho e a situação real.Então criar uma escala é criar uma razão.Veja em baixo que a razão entre esses dois tamanhos é exatamente a escala.

                                            

Agora observe a escala desse mapa, 1:36.000.000, isso quer dizer que 1 cm no mapa corresponde a 36.600.000 cm do tamanho real.Vejamos outros exemplos:

• 1:1000(cm) que quer dizer que 1 cm no desenho corresponde a 1000 cm ou     10 m no tamanho real.
• 1:250000 quer dizer que 1 cm no desenho equivale a 250000 cm ou 2,5 km no tamanho real.  

Então vimos que:

• A razão entre dois números A e B (nessa ordem) é dada por:  
• Se A e B são proporcionais a C e D, então:   
• Use a regra de três apenas quando as grandezas envolvidas forem proporcionais!
• Uma escala E é uma razão onde:
• E = 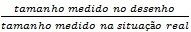 (mesma unidade) 

Questão para fixar o conteúdo de escalas:

2.(ENEM-2011) Para uma atividade realizada no laboratório de Matemática, um aluno precisa construir uma maquete da quadra de esportes da escola que tem 28 m de comprimento por 12 m de largura. A maquete deverá ser construída na escala de 1: 250.

Que medidas de comprimento e largura, em cm, o aluno utilizará na construção da maquete?

(a)4,8 e 11,2
(b)7,0 e 3,0
(c)11,2 e 4,8
(d)28,0 e 12,0
(e)30,0 e 70,0

Grandezas diretamente e inversamente proporcionais 

O silogismo é uma estrutura lógica de pensamento nascente do filosofo Aristóteles, se caracteriza pelo método indutivo, sendo uma comparação de uma coisa com outra por meio de uma interseção. Vejamos um exemplo abaixo contraditório ao silogismo como a celebre frase de Sócrates e mais adiante um exemplo que obedece a regra.

‘’ Só sei que nada sei ‘’

Premissa maior: Não sei de nada

Premissa menor: Sei que não sei

Conclusão: Podemos perceber que a frase não obedece a lógica, pois se eu afirmo que nada sei, como posso afirmar que sei que não sei.

‘’ Todos os humanos são mortais, todos os filósofos são humanos, então todos os filósofos são mortais.’’

Premissa maior: Todos os humanos são mortais

Premissa menor: todos os filósofos são humanos

Conclusão: então todos os filósofos são mortais

Agora você pode perceber que o método indutivo consiste em uma premissa geral (algo como uma lei que será muito difícil contestar), para chegar à conclusão de uma premissa menor. Mas o que o silogismo tem em comum com grandezas (tudo aquilo que pode ser medido) diretamente ou inversamente proporcionais?

Vamos pensar em um queijo cheio de buracos, cada buraco ocupa o lugar onde haveria queijo. Dessa forma quanto mais buracos, menos queijo, o que temos aqui é uma grandeza inversamente proporcional usando o silogismo ou seja a lógica. Agora que você já aprendeu a brincar com o silogismo em grandezas vamos compreende-las melhor.

• Na matemática, a razão estabelece uma comparação entre duas grandezas, sendo o coeficiente entre dois números.
• Já a proporção é determinada pela igualdade entre duas razões, ou ainda, quando duas razões possuem o mesmo resultado.

Diretamente Proporcionais, isso ocorre quando a razão entre os valores da 1° grandeza é igual a razão entre os valores da 2°. Ou seja uma varia de acordo com a outra. Se uma aumenta a outra também aumenta.
Ex:Um automóvel viaja com velocidade igual a 60 km/h percorrendo 100km.Durante o mesmo tempo, um outro automóvel viaja a 80km/h. Quantos quilômetros esse automóvel percorreu?

Quanto maior a velocidade dos automóveis maior será a distância percorrida, se a velocidade for menor a distância também será. Assim a velocidade e a distância são grandezas diretamente proporcionais. Então podemos multiplicar em crus.

Inversamente Proporcionais: Se uma aumenta a outra diminui na mesma proporção.

EX:Um automóvel viaja com a velocidade constante igual a 60 km/h, durante 2 horas. Para percorrer o trajeto da volta, a uma velocidade de 80km/h, quantas horas serão necessárias?

Perceba que quanto maior a velocidade menor será o tempo de viajem. Podemos dizer que nas grandezas inversamente proporcionais, uma aumentas e a outra diminui na mesma proporção. Assim não se pode multiplicar em cruz, você terá que multiplicar na horizontal ou inverter as distâncias.

Questão para fixar o conteúdo de grandezas diretamente e inversamente proporcionais:

3. (ENEM-2014) A Companhia de Engenharia de Tráfego (CET) de São Paulo testou em 2013 novos radares que permitem o cálculo da velocidade média desenvolvida por um veículo em um trecho da via.

As medições de velocidade deixariam de ocorrer de maneira instantânea, ao se passar pelo radar, e seriam feitas a partir da velocidade média no trecho, considerando o tempo gasto no percurso entre um radar e outro. Sabe-se que a velocidade média é calculada como sendo a razão entre a distância percorrida e o tempo gasto para percorrê-la.

O teste realizado mostrou que o tempo que permite uma condução segura de deslocamento no percurso entre os dois radares deveria ser de, no mínimo, 1 minuto e 24 segundos. Com isso, a CET precisa instalar uma placa antes do primeiro radar informando a velocidade média máxima permitida nesse trecho da via. O valor a ser exibido na placa deve ser o maior possível, entre os que atendem às condições de condução segura observadas.

Disponível em: www1.folha.uol.com.br. Acesso em: 11 jan. 2014 (adaptado).

 A placa de sinalização que informa a velocidade que atende a essas condições é:

4.(ENEM-2013)Muitos processos fisiológicos e bioquímicos, tais como batimentos cardíacos e taxa de respiração, apresentam escalas construídas a partir da relação entre superfície e massa (ou volume) do animal. Uma dessas escalas, por exemplo, considera que “o cubo da área S da superfície de um mamífero é diretamente proporcional ao quadrado de sua massa M”.

HUGHES-HALLETT, D. et al. Cálculo e aplicações. São Paulo: Edgard Blücher, 1999 (adaptado).

Isso é equivalente a dizer que, para uma constante k > 0, a área S pode ser escrita em função de M por meio da expressão: 

Mostrando grandezas diretamente e inversamente proporcionais na forma algébrica

Diretamente Proporcionais: Perceba que a razão da divisão desses números são constantes, quando dividimos o x pelo y sempre obtemos 2. Então y é diretamente proporcional a x ou seja y/x= k (constante)

(y/x = 2/1=2,  4=2 =2, 6/3 =2,10/5=2, 22=11=2) 

Ex: y é diretamente proporcional a x ou seja y/x=k

y é diretamente proporcional a  x²  ou seja y/x² =k

y³ é diretamente proporcional a x²  ou seja y³ /x²=k

Inversamente Proporcionais:Quando multiplicamos o y pelo x obtemos produtos contantes ( 2.1=2, 1.2=2, 1/2.4=2, 1/4.8=2, 1/6.12=2). Assim podemos dizer que y.x= k

Ex: y é diretamente proporcional a x ou seja y.x=k
y é diretamente proporcional a  x²  ou seja y.x² = constante
y³ é diretamente proporcional a x²  ou seja y^{3 .}x²=k

Respostas das questões de fixação:1.d , 2.c, 3.c, 4.d

Vamos praticar um pouco?Acesse o link para ir para a pagina de exercícios:

https://nossodiariodoenem.blogspot.com/2018/07/exercicios-de-matematica-razao-e.html